Chap1 Using neural nets to recognize handwritten digits 识别手写数字
人的主要视皮层(V1)包含1.4亿神经元,上百亿的神经连接。这仅仅是V1,涉及到视觉处理的包括V2,V3,V4和V5.
如通过创建规则的方式识别,很容易陷入无穷尽的例外和特例中。神经网络的方式采用了不同的方式。
目前识别手写数字准确率非常高,银行用其来识别支票,邮局用其来识别邮编。
Perceptrons 感知机??

A perceptron takes several binary inputs, $x_1,x_2,x_3$ and produces a single binary output. Rosenblatt 提出用“加权和”计算输出结果,并根据某个阈值来判断输出是1还是0:
$$ output = \left{\begin{matrix}0, \text{if } \sum{j} w_j,x_j \leq threshold \1, \text{if } \sum{j} w_j,x_j > threshold
\end{matrix}\right. (1)
$$
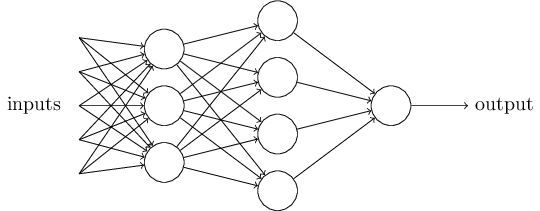
注意,每个perceptron只有一个output,上图中虽然看起来有多个输出结果,实际上只有一个,箭头所代表的是其输出结果作为下一层的input。
公式(1)可以用向量的方式简化,另外将阈值移到等式左边 $b \equiv -threshold$,b称为bias
$$ output = \left{\begin{matrix}0,\text{if } w \cdot x - b\leq 0 \1,\text{if } w \cdot x - b > 0
\end{matrix}\right. (2)
$$
Sigmoid neurons
训练模型,期望的是weights(or bias)略微改变,则输出结果也略微改变;这样就可以通过对w和b的调整来是的模型有更好的结果。但是由Perceptrons构成的网络做不到这一点。
Sigmoid神经元可以解决这个问题。输出不再是0或1,而是在0 - 1之间
$\sigma(z)\equiv \frac{1}{1+e^(-z)}$
Sigmoid neurons和perceptrons非常类似;a smoothed out perceptron。这种“平滑性”是最关键的点,其具体的形式并不特别重要。
$\Delta \mbox{output}$ 是 $\Delta w_j$ 和 $\Delta b$ 的线性组合。
采用Sigmoid函数是因为其形状,而非具体形式,那为什么要用这一个函数呢?主要是因为计算导数上的便捷。因此是非常常用的激活函数。
The Architecture of Neural Networks
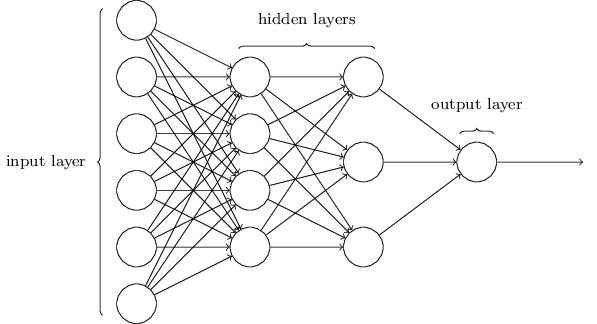
Note: 出于历史惯例,上述网络通畅叫做Multilayer perceptrons or MLPs, 尽管其实是有sigmoid neuron构成的。
输入层和输出层一般都是简明了当的,隐藏层的设计则不同,没有简单的法则。
feedforward neural networks: 前一层的输出作为后一层的输入,信息总是向前的,不会向后,没有循环。
sigmoid神经网络不允许循环,因为如果允许的话,sigmoid的输出会影响输入。
其他的神经网络模型允许循环,叫做 recurrent neural networks. 神经元fire的时间有限,可以影响其它神经元,在一定时间后会fire,持续一段时间。一个神经元的输出结果在一定时间后可能会影响其自身的输出,但是这种影响不是同时的,因此这种循环不会造成问题。
recurrent neural networks目前影响力小于feedforward networks, 部分是因为其算法效果差一些。但也是非常有趣的模型,因为它的运作方式更接近于人脑的运作方式.
A Simple Network to Classify Handwritten digits
- 将每个数字分离出来
- 识别每个数字
可以用(2)来衡量(1)的结果。
Learning with Gradient Decent
为什么要最小化cost,而不是最大化准确率? 因为准确率是一个针对weights和bias的平滑的函数。大多数适合,微调w和b不会改变准确率,这样就很难通过调整w和b来改善模型。而用cost function(比如均方差)这种平滑的函数,可以通过改变w和b来改进模型。因此先最小化cost,然后才会计算准确率。
一种思路是用微积分找到最小值,但是如果变量增加的话(神经网络往往有非常多的变量),用微积分的方法变得非常困难,甚至不可行。
Implementing our network to classify digits
Change Logs
- 2017.10.14 创建
- 2017.11.12 增加内容